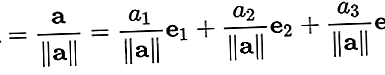数学と物理学のベクトルは、大きさと方向を持つ幾何学的オブジェクトとして定義できます。ベクトルは矢印で表されます。矢印の基部はベクトルのキャッチポイント(開始点)を示し、矢印の長さはベクトルのサイズまたは値を示します(矢印が長いほど、値は大きくなります。ベクトルの値、およびその逆)、矢印はベクトルの方向を示します。

書面では、ベクトルが点Aで始まり、点Bで終わる場合、その上に次のような線/矢印がある小文字で書くことができます。 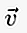 または
または 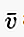 またはまた:
またはまた:
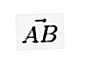
ベクトルの種類
数学のベクトルは、次の4つのタイプに分けられます。
位置ベクトル
開始点が0(0,0)で、終了点がA(a1、a2)であるベクトル。
ゼロベクトル
「ベクトルゼロ」(ヌルベクトル またはゼロベクトル)は、長さが「ゼロ」のベクトルです。このベクトル座標での書き込みは(0,0,0)であり、通常は記号が付けられます  、または0。このベクトルは、正規化できないという点で他のベクトルとは異なります(つまり、単位ベクトルがゼロベクトルの倍数になることはありません)。ベクトルの数はどのベクトルでもゼロですa ですa (あれは、0+a=a).
、または0。このベクトルは、正規化できないという点で他のベクトルとは異なります(つまり、単位ベクトルがゼロベクトルの倍数になることはありません)。ベクトルの数はどのベクトルでもゼロですa ですa (あれは、0+a=a).
ゼロベクトルには明確なベクトル方向がありません。
単位ベクトル
長さが「1」のベクトルです。通常、単位ベクトルは方向を示すためにのみ使用されます。任意の長さのベクトルを長さで割って、単位ベクトルを取得できます。これは、ベクトルの「正規化」として知られています。単位ベクトルは、次のように小文字の「a」の上に「キャップ」で示されることがよくあります。â.
ベクトルを正規化するにはa = [a1, a2, a3]、ベクトルを長さで割る||a||。そう:
基本ベクトル
互いに垂直な単位ベクトル。 2次元空間ベクトル(R2)には2つの基本ベクトルがあります。 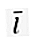 =(1、0)および
=(1、0)および 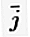 = (0, 1).
= (0, 1).
2つのベクトルの類似性
2つのベクトルが同じ長さと方向を持っている場合、それらは同じであると言われます

2つのベクトルの配置
2つのベクトルを表す線が平行である場合、2つのベクトルは平行(平行)と呼ばれます。
ベクトル演算
スカラー乗法
ベクトルにスカラーを掛けると、ベクトルも生成されます。結果のベクトルは次のようになります。
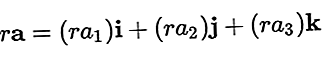
ベクトル加算とベクトル減算
ベクトルの例として a=a1私 + a2j + a3k そしてb=b1私 + b2j + b3k
プラスbの結果は次のとおりです。 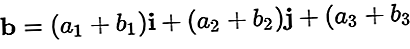
+記号を-記号に置き換えることによってもベクトル削減が適用されます